Stationarity

In time series, stationarity means dependence of previous observations “declines” over time, or formally, assumes the process’s statistical properties are time-invariant.

• Strict Stationarity: The joint distribution of $\{Y_{t_1},\dots ,Y_{t_n}\}$ equals that of $\{Y_{t_1-k},\dots ,Y_{t_n-k}\}$ for all $t_i$ and $k$. Implies constant mean and variance, and ${\gamma }_{t,s}={\gamma }_{0,|t-s|}$.
• Weak (Second-Order) Stationarity: Requires constant mean and ${\gamma }_{t,t-k}={\gamma }_{0,k}$ for all $t$ and $k$. Used throughout the book unless specified otherwise.

For stationary processes, we denote ${\gamma }_k=\mathrm{Cov}(Y_t,Y_{t-k})$, ${\rho }_k=\frac{{\gamma }_k}{{\gamma }_0}$, with properties: ${\gamma }_0=\mathrm{Var}(Y_t)$, ${\rho }_0=1$, ${\gamma }_k={\gamma }_{-k}$, $|{\rho }_k|\le 1$.

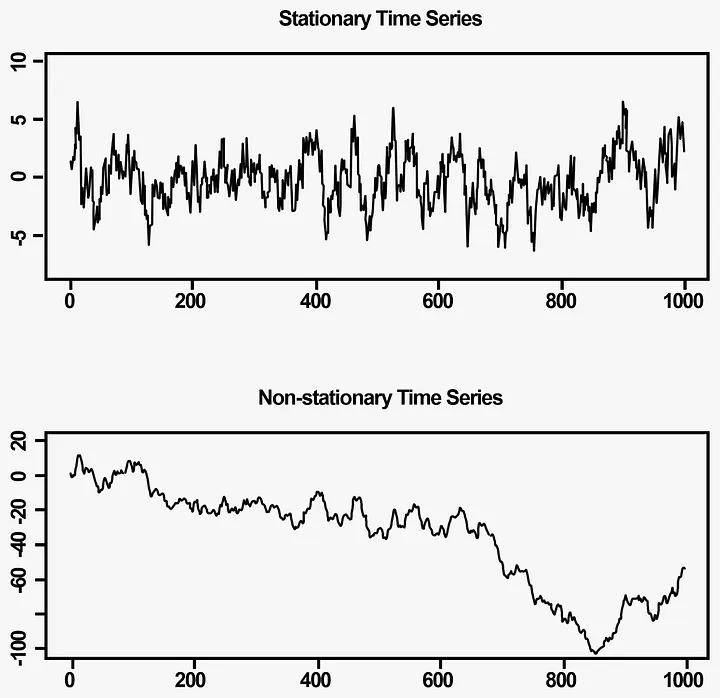
TODO Common solution to stationary data is to use differencing. Differencing works for these: 

But not these: 

See also

• https://www.youtube.com/watch?v=aIdTGKjQWjA

Examples

White Noise

Defined as $\{e_t\}$, i.i.d. with $E(e_t)=0$, $\mathrm{Var}(e_t)={\sigma }_e^2$:

Property	Expression
Mean	${\mu }_t=0$
Autocovariance	${\gamma }_k=\{\begin{array}{ll}{\sigma }_e^2& ,k=0\\ 0& ,k\ne 0\end{array}$
Autocorrelation	${\rho }_k=\{\begin{array}{ll}1& ,k=0\\ 0& ,k\ne 0\end{array}$
Stationarity	Strict and weak

Random Cosine Wave

Defined as $Y_t=\cos [2\pi (\frac{t}{12}+\Phi )]$, where $\Phi \sim \text{Uniform}(0,1)$:

Property	Expression
Mean	${\mu }_t=0$
Autocovariance	${\gamma }_{t,s}=\frac{1}{2}\cos [2\pi (\frac{t-s}{12})]$
Autocorrelation	${\rho }_k=\cos (2\pi \frac{k}{12})$
Stationarity	Weak

Nonstationary Example: Random Walk

Variance $t{\sigma }_e^2$ and covariance ${\gamma }_{t,s}=t{\sigma }_e^2$ (for $t\le s$) depend on $t$, not just $|t-s|$, so not stationary. Differencing $\nabla Y_t=Y_t-Y_{t-1}=e_t$ yields a stationary process (white noise).

See Random Walk